November 11, 2024 by Marcus Strom, University of Sydney
Collected at: https://phys.org/news/2024-11-compact-error-efficient-quantum-hard.html
Two quantum information theorists at the University of Sydney Nano Institute have solved a decades-old problem that will require fewer qubits to suppress more errors in quantum hardware.
University of Sydney quantum researchers Dominic Williamson and Nouédyn Baspin have revealed a transformative new architecture for managing errors that emerge in the operation of quantum computers.
Their innovative theoretical approach promises to not only enhance the reliability of quantum information storage but also significantly reduce the physical computing resources needed to create “logical qubits” (or “quantum switches” that can perform useful calculations). This should lead to the development of a more compact quantum hard drive.
Lead author Dr. Williamson from the University of Sydney Nano Institute and School of Physics said, “There remain significant barriers to overcome in the development of a universal quantum computer. One of the biggest is the fact we need to use most of the qubits—quantum switches at the heart of the machines—to suppress the errors that emerge as a matter of course within the technology.
“Our proposed quantum architecture will require fewer qubits to suppress more errors, liberating more for useful quantum processing,” said Dr. Williamson, who is currently working for 12 months as a quantum researcher at IBM.
The study has been published in Nature Communications.
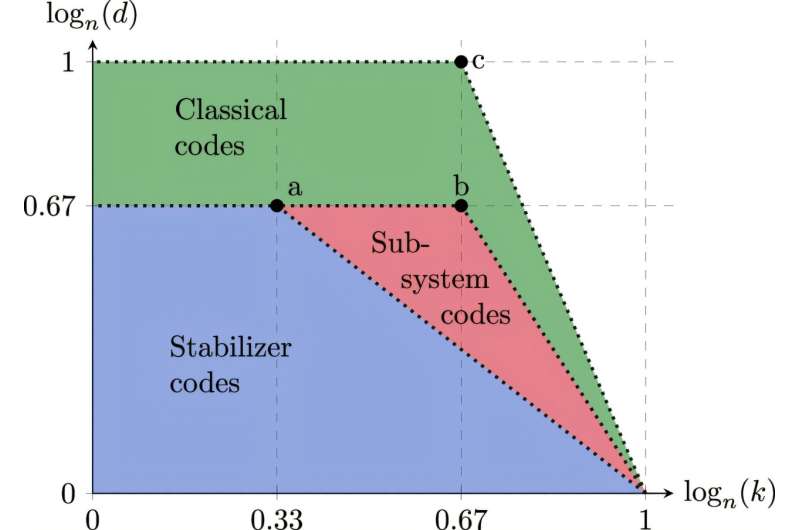
At the heart of their theoretical architecture is a three-dimensional structure that allows for quantum error correction across two-dimensions. Current error correction architecture, also constructed within a 3D system of qubits, works to reduce errors in just one dimension along a single line of connected qubits.
Error correction is performed by writing code that operates through the qubit structure, a latticework of how the quantum switches are organized. The objective is to win an “arms race” where physical qubits are used to suppress errors as they emerge, by using as few qubits as possible to reduce errors.
Dr. Williamson said, “Current 3D codes in a block of dimensions L x L x L can only manage L errors. Our codes can handle errors that scale like L2 (LxL)—a significant improvement.”
It has been known for more than a decade that a three-dimensional quantum error correction architecture (LxLxL) had an upper limit of LxL, but no such codes had been discovered.
Ph.D. student and co-author Baspin said, “This means that we have discovered new states of quantum matter in three dimensions that have properties never seen before.”
Quantum computers promise to solve complex problems that are currently beyond the reach of classical computers. However, one of the major challenges in realizing practical quantum computing is the need for robust error correction mechanisms.
Traditional quantum error correction methods, such as the widely studied surface code, have limitations in terms of scalability and resource efficiency.
Williamson and Baspin’s research introduces a three-dimensional architecture that effectively manages quantum errors within two-dimensional layers. By leveraging this three-dimensional topological code, the researchers have demonstrated that it is possible to achieve optimal scaling while significantly reducing the number of physical qubits needed. This advance is crucial for the development of scalable quantum computers, as it allows for a more compact construction of quantum memory systems.
By reducing the physical qubit overhead, the findings pave the way for the creation of a more compact quantum hard drive—an efficient quantum memory system capable of storing vast amounts of quantum information reliably.
Quantum theorist and Director of the University of Sydney Nano Institute, Professor Stephen Bartlett, said, “This advancement could help transform the way quantum computers are built and operated, making them more accessible and practical for a wide range of applications, from cryptography to complex simulations of quantum many-body systems.”
More information: Dominic J. Williamson et al, Layer codes, Nature Communications (2024). DOI: 10.1038/s41467-024-53881-3
Journal information: Nature Communications

Leave a Reply