October 13, 2024 by Ingrid Fadelli , Phys.org
Collected at: https://phys.org/news/2024-10-protocols-hamiltonian-parameters-superconducting-quantum.html
Researchers at Freie Universität Berlin, University of Maryland and NIST, Google AI, and Abu Dhabi set out to robustly estimate the free Hamiltonian parameters of bosonic excitations in a superconducting quantum simulator. The protocols they developed, outlined in a paper pre-published on arXiv, could contribute to the realization of highly precise quantum simulations that reach beyond the limits of classical computers.
“I was taking part in a conference in Brazil when I received a call from friends of the Google AI team,” Jens Eisert, first author of the paper, told Phys.org.
“They were trying to calibrate their Sycamore superconducting quantum chip with methods of Hamiltonian learning and encountered severe obstacles and were calling for help. Having worked a lot both on analog quantum simulation ideas and on systems identification methodology, I was truly intrigued.”
When Eisert first started considering the problem posed to him by his friends, he thought it should be easy to solve. Yet he soon realized that it would be more challenging than expected, as the frequencies of the Hamiltonian operator in the team’s system were not recovered accurately enough to identify unknown Hamiltonian from the available data.
“I invited two extremely smart Ph.D. students, Ingo Roth and Dominik Hangleiter, and together, we quickly found a solution using superresolution ideas—in principle, that is, until data came in,” said Eisert.
“It then took another few years until we understood how to make ideas of Hamiltonian learning robust enough so that they can be applied to actual large-scale experiments.
“In the meantime, another Ph.D. student had joined, Jonas Fuksa, and the other two had long graduated. It helped that Pedram Roushan, the experimental lead of the Google AI efforts, remained persistent and provided excellent data. In the end, years later, we found a solution to the question raised in the Zoom call years earlier.”
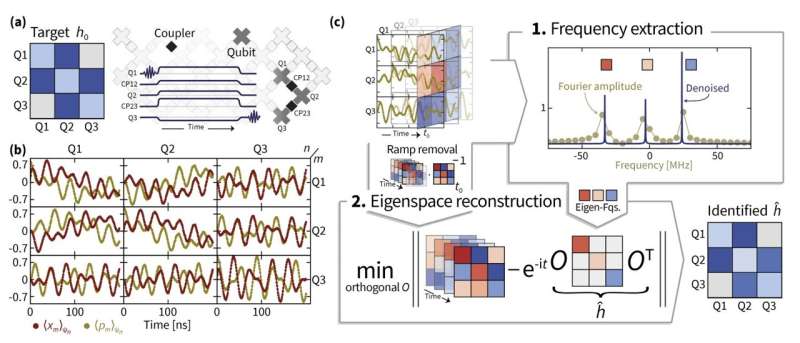
To learn the Hamiltonian dynamics of a superconducting quantum simulator, Eisert and his colleagues employed various techniques. Firstly, the researchers used superresolution, a method to enhance the resolution of eigenvalue estimation, to attain the correct Hamiltonian frequencies.
They then used a technique known as manifold optimization to recover the eigenspaces of the Hamiltonian operator, actually recovering the Hamiltonian. Manifold optimization entails the use of specialized optimization algorithms to tackle complex problems for which variables lie on a manifold (smooth and curved space), rather than in a standard Euclidean space.
“To attain robust estimates, we combined a number of ideas,” explained Eisert.
“Even to understand the processes of switching on and off was important, as these processes are not perfect and instantaneous (and not even unitary), so if one tries to fit a Hamiltonian evolution that is in parts not Hamiltonian at all, one gets a mess. In the end, new methods of signal processing that we called TensorEsprit allowed for a robust recovery up to large system sizes.”

In their paper, the researchers introduce a new technique for implementing super-resolution, which they dubbed TensorEsprit. By combining this technique with a manifold optimization method, they were able to robustly identify the Hamiltonian parameters for up to 14 coupled superconducting qubits distributed across two Sycamore processors.
“In the early phase, it was important to understand the significance of methods of Hamiltonian learning altogether,” said Eisert.
“Then one can recover eigenspaces meaningfully only if eigenvalues are extremely accurately known. In the later phases of the project, we understood in a hard way why there are so few publications that present data from Hamiltonian learning out there: it is just very difficult to make it work for practical data.”
The initial tests run by the researchers suggest that their proposed techniques could be scalable and robustly applicable to large quantum processors. Their work could inspire the development of similar approaches for characterizing the Hamiltonian parameters of quantum processors.
As part of their next studies, Eisert and his colleagues plan to apply their methods to interacting quantum systems. They are also working on applying similar ideas derived from tensor networks to quantum systems comprised of cold atoms, which were first introduced by physicist Immanuel Bloch.
“I think that this field will become important in the future,” added Eisert. “An old and yet often underappreciated question is that of what a Hamiltonian of a system actually is. This question is already asked in the basic lectures on quantum mechanics. Because even if it characterizes the system, it is often assumed to be known, an assumption that is often not the case.
“At the end of the day, experiments only ever produce data, and so, in quantum mechanics, you only have predictive power if you know the Hamiltonian exactly. So, the question arises as to how you can learn it from data.”
In addition to contributing to the conceptual understanding of Hamiltonian operators, the researchers’ future studies could inform the development of quantum technologies. By aiding the characterization of analog quantum simulators, in fact, they could open new avenues for the realization of high-precision quantum simulations.
“Analog quantum simulation allows complex quantum systems and materials to be researched in a new way by recreating them under extremely precise conditions in the laboratory,” explained Eisert.
“Yet this idea only makes sense—and is associated with precise predictions—if you know the Hamiltonian that characterizes the system exactly.”
More information: Dominik Hangleiter et al, Robustly learning the Hamiltonian dynamics of a superconducting quantum processor, arXiv (2024). DOI: 10.48550/arxiv.2108.08319
Journal information: arXiv

Leave a Reply