September 24, 2024 by Ingrid Fadelli , Phys.org
Collected at: https://phys.org/news/2024-09-team-emergence-fluctuating-hydrodynamics-chaotic.html
Researchers at Ludwig-Maximilians-Universität, Max-Planck-Institut für Quantenoptik, Munich Center for Quantum Science and Technology (MCQST) and the University of Massachusetts recently carried out a study investigating the equilibrium fluctuations in large quantum systems. Their paper, published in Nature Physics, outlines the results of large-scale quantum simulations performed using a quantum gas microscope, an experimental tool used to image and manipulate individual atoms in ultracold atomic gases.
“Imagine that you have a large number of particles in a box and want to predict how the system will evolve in the future,” Julian Wienand, co-author of the paper, told Phys.org. “You know the physics of these particles and how they interact with each other. So, in principle, you could set up a simulation outputting the movement of every single particle. However, in practice, because there are so many particles to keep track of, the simulation might fail due to a lack of computational resources. Fortunately, there is a way to move forward: hydrodynamics.”
Hydrodynamics theory offers quantum physicists with an alternative route for simulating the interactions between particles in large systems. If a system is chaotic, in fact, researchers can assume that the particles will interact in ways that will ensure a state of local thermal equilibrium.
“This allows us to come up with a macroscopic description and essentially describe the particles as a continuous density field that follows simple differential equations,” said Wienand. “In general, such a density field may fluctuate, because microscopically it is made up of fast-moving particles. Since these fluctuations are random, we can think of them as white noise, and integrating them into our differential equations gives us fluctuating hydrodynamics (FHD).”
FHD is an extension of classical hydrodynamics theory, which also predicts the effects of thermal fluctuations in a system. By also accounting for small-scale fluctuations, this extended theoretical framework allows physicists to effectively describe and compute complex systems.
Overall, FHD theory suggests that the entire evolution of complex systems depends on a few quantities, such as a so-called diffusion constant. While this theory has been used to study a wide range of classical systems, it is unclear whether it also applies to chaotic quantum systems.
“Quantum systems are fundamentally different from their classical counterparts because their constituent particles can exhibit quantum phenomena like entanglement, which defy everyday intuition,” said Wienand. “They are also much harder to calculate, so being able to describe them using FHD could help us understand such systems better and make predictions about them.”
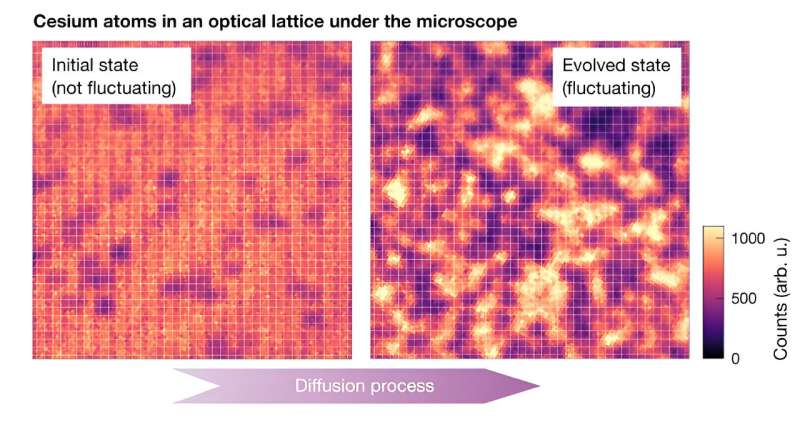
Wienand and his colleagues carried out various quantum simulations using a 133Cs (cesium) quantum gas microscope. Essentially, the team trapped ultracold Cs atoms in an optical lattice (i.e., a lattice created by laser light). This produced a system comprised of quantum particles interacting with each other, also known as a quantum many-body system.
“Thanks to our microscope, we can take snapshots of this system with single-site resolution, meaning that we can detect which lattice sites are occupied by an atom and which are empty,” explained Wienand. “This is crucial for counting the number of particles in certain areas of the system and measuring the statistics of this observable, including the atom number fluctuations.”
The researchers prepared their system in an excited state by placing the Cs atoms in specific sites, producing a regular pattern. They then abruptly reduced the depth of the lattice, which allowed atoms to start moving around and interacting with one another.
“Consequently, the quantum many-body system undergoes a diffusion process and thermalizes,” said Wienand. “During the thermalization process, we track the evolution of fluctuations over time and watch them grow. Comparing the growth speed of these fluctuations (and other observables) with theory allows us to conclude that the system is well described by FHD, and further, measure the diffusion constant.”
The recent study by this team of researchers offers the first demonstration that FHD theory can be used to describe chaotic quantum systems both qualitatively and quantitatively. This was so far achieved in a simple experimental setting, which could ultimately be applied to the study of various chaotic quantum systems.
“In our case, this means that the entire microscopic quantum physics can be macroscopically approximated by a simple classical diffusive FHD model, and that the entire macroscopic dynamics of the system is described by a single quantity: a diffusion constant,” said Wienand. “This provides us with new tools for studying chaotic quantum systems and making predictions about their seemingly complex behavior, at least on a macroscopic scale.”
The findings gathered by the researchers suggest that a paradigm that is well-established for classical systems also applies to quantum systems. This is the idea that even if a system’s microscopic physics are complex and chaotic, its macroscopic behavior may in fact be very simple.
“Another surprising fact about the diffusion constant is that it is an equilibrium property of the system,” said Wienand. “However, when we measure, the quantum many-body system is out of equilibrium. FHD establishes a relationship between equilibrium and out-of-equilibrium settings. Our results take advantage of this relationship and use it as a new way to obtain the diffusion constant.”
Wienand and his colleagues are currently conducting further quantum simulations using their Cs quantum gas microscope. These new studies could gather further insight about the mechanisms underpinning quantum many-body dynamics.
“Open questions for this next study will include: How do fluctuations behave in systems that do not thermalize? How about higher momenta beyond the fluctuations, such as skewness and kurtosis? And, can FHD be adapted to include and correctly describe more complex observables and/or in more exotic systems?” added Wienand.
“Our results have provided a first indication of the large potential of FHD in describing quantum systems, but more experiments need to follow in order to assess the range and the limitations of FHD in the quantum realm.”
More information: Julian F. Wienand et al, Emergence of fluctuating hydrodynamics in chaotic quantum systems, Nature Physics (2024). DOI: 10.1038/s41567-024-02611-z.
Journal information: Nature Physics

Leave a Reply