September 6, 2024 by University of Rhode Island
Collected at: https://phys.org/news/2024-09-theoretical-quantify-vital-quantum-properties.html
The foundation of nearly all quantum information applications—such as computation and communication—rely on the quantum properties of superposition and entanglement.
In quantum computers—which hold the promise of performing complex calculations that today’s classical computers can’t handle—superposition and entanglement go hand in hand. While superposition allows a physical system—like a particle—to be in multiple states simultaneously, entanglement links particles, allowing them to form an inseparable state, even when they are separated by a large distance.
“They are the fundamental properties of quantum mechanics, the determining properties for many applications,” said Wenchao Ge, assistant professor of physics at the University of Rhode Island, whose theoretical research explores fundamental issues in quantum mechanics. “Without superposition and entanglement, no quantum-enhanced application would exist.”
In recent theoretical research, Ge and collaborators Jiru Liu and M. Suhail Zubairy, members of the Institute for Quantum Science and Engineering at Texas A&M University, explored the relationship between the two fundamental resources to quantum physics.
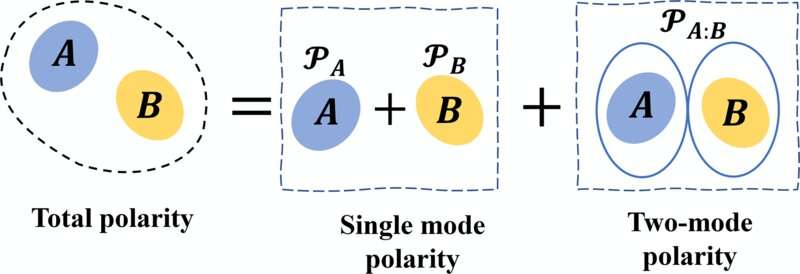
They established a single way to quantify the two properties, defining a mathematical description of each. Their paper, “Classical-Nonclassical Polarity of Gaussian States,” was published in Physical Review Letters.
“It’s theoretical proof that the two properties—superposition and entanglement—can be interchanged quantitatively,” said Ge. “Our work discovers an important quantitative relation between these two fundamental quantum effects for a large class of quantum states. This work opens a new direction of research in quantifying these resources for quantum information processing.”
The ability to quantify the properties allows for the conversion of these two resources from one state to the other. “Sometimes in quantum mechanics, one resource may be difficult to prepare,” said Ge. “If you could have the other type of resource, you can convert between these resources.”
In the field of quantum mechanics, there has been interest in understanding and application of nonclassical resources—resources that do not have a classical counterpart, such as a particle in a state with a negative probability. But research has fallen short in coming up with a satisfactory unified evaluation of both properties, Ge said.
The researchers wanted to explore the internal relationship between the two quantum properties, which determine many high-level quantum applications such as computation, communication and sensing. To do so, they looked at Gaussian states, a large class of states in quantum mechanics known for their ease in reproducing and manipulation during quantum information experiments.
Previous studies have looked at quantitative relationships of the two properties for two-mode or three-mode (two or three particle) Gaussian states. The team advanced the research, proposing a single measure for quantum superposition in one-particle systems and entanglement between multiple particles (two or three particle modes).
The new measure, “classical-nonclassical polarity,” is shown to unify the two effects quantitatively for a large class of Gaussian states, Ge said.
Ge said the work can form a foundation for exploring other quantum properties for information applications such as quantum sensing and computing.
“This is the first step in finding a quantitative relation between these two properties,” said Ge. “For Gaussian states, we have only proved this relationship up to three modes. It may be useful to study four, five or even more bipartite. We conjecture such a quantitative relation even beyond Gaussian states.
“For physics research, we want to see what are the properties, what are the fundamental principles,” he added. “If we discover a fundamental principle, there could be far-reaching applications.”
More information: Jiru Liu et al, Classical-Nonclassical Polarity of Gaussian States, Physical Review Letters (2024). DOI: 10.1103/PhysRevLett.132.240201. On arXiv: DOI: 10.48550/arxiv.2310.12104
Journal information: Physical Review Letters , arXiv

Leave a Reply