SEPTEMBER 22, 2022 by Michael Hallermayer, Universität Augsburg
An international team of physicists, with the participation of the University of Augsburg, has for the first time confirmed an important theoretical prediction in quantum physics. The calculations for this are so complex that they have hitherto proved too demanding even for supercomputers. However, the researchers succeeded in simplifying them considerably using methods from the field of machine learning. The study improves the understanding of fundamental principles of the quantum world. It has been published in the journal Science Advances.
The calculation of the motion of a single billiard ball is relatively simple. However, predicting the trajectories of a multitude of gas particles in a vessel which are constantly colliding, being slowed down and deflected, is way more difficult. But what if it is not even at all clear exactly how fast each particle is moving, so that they would have countless possible velocities at any given time, differing only in their probability?
The situation is similar in the quantum world: Quantum mechanical particles can even have all potentially possible properties simultaneously. This makes the state space of quantum mechanical systems extremely large. If you aim to simulate how quantum particles interact with each other, you have to consider their complete state spaces.
“And that is extremely complex,” says Prof. Dr. Markus Heyl from the Institute of Physics at the University of Augsburg. “The computational effort increases exponentially with the number of particles. With more than 40 particles, it is already so large that even the fastest supercomputers are unable to cope with it. This is one of the grand challenges of quantum physics.”
Neural networks make the problem manageable
To simplify this problem, Heyl’s group used methods from the field of machine learning—artificial neural networks. With these, the quantum mechanical state can be reformulated. “This makes it manageable for computers,” explains Heyl.
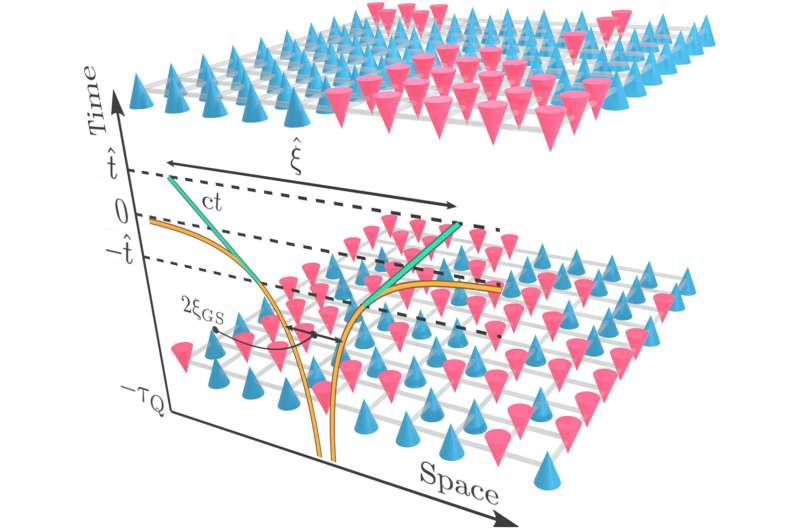
Using this method, the scientists have investigated an important theoretical prediction that has remained an outstanding challenge so far—the quantum Kibble-Zurek mechanism. It describes the dynamical behavior of physical systems at what is called a quantum phase transition. An example of a phase transition from the macroscopic and more intuitive world is the transition from water to ice. Another example is the demagnetization of a magnet at high temperatures.
If you go the other way round and cool the material , the magnet starts to form again below a certain critical temperature. However, this does not happen evenly across the entire material. Instead, many small magnets with differently aligned north and south poles are created at the same time. Thus, the resulting magnet is actually a mosaic of many different, smaller magnets. Physicists also say that it contains defects.
The Kibble-Zurek mechanism predicts how many of these defects are to be expected (in other words, how many mini-magnets the material will eventually be composed of). What is particularly interesting is that the number of these defects is universal and thus independent of microscopic details. Accordingly, many different materials behave precisely identically, even if their microscopic composition is completely different.
The Kibble-Zurek mechanism and the formation of galaxies after the Big Bang
The Kibble-Zurek mechanism was originally introduced to explain the formation of structure in the universe. After the Big Bang, the universe was initially completely homogeneous, which means that the hosted matter was distributed perfectly evenly. For a long time it has been unclear how galaxies, suns or planets could have formed out of such a homogeneous state.
In this context the Kibble-Zurek mechanism provides an explanation. As the universe was cooling down, defects developed in a similar way to magnets. In the meantime these processes in the macroscopic world are well understood. But there is one type of phase transition for which it has not yet been possible to verify the validity of the mechanism—namely the quantum phase transitions already mentioned before. “They only exist at the absolute zero temperature point of -273 degrees Celsius,” explains Heyl. “So the phase transition does not take place during cooling, but through changes in the interaction energy—you could think, perhaps, of varying the pressure.”
The scientists have now simulated such a quantum phase transition on a supercomputer. They were thus able to show for the first time that the Kibble-Zurek mechanism also applies in the quantum world. “That was by no means an obvious conclusion,” says the Augsburg physicist. “Our study allows us to better describe the dynamics of quantum mechanical systems of many particles and hence to understand more precisely the rules that govern this exotic world.”
More information: Markus Schmitt et al, Quantum phase transition dynamics in the two-dimensional transverse-field Ising model, Science Advances (2022). DOI: 10.1126/sciadv.abl6850
Journal information: Science Advances
Provided by Universität Augsburg
Collected at:

Leave a Reply