16 Feb 2022 by Pradeep Niroula
Hyped as the solution to many problems – both hard and easy – quantum-enhanced optimization is a burgeoning research field. But with untrainable circuits, “barren plateaus” and deceptive local minimas, nature itself may prevent the use of quantum solutions for hard problems, as Pradeep Niroula explains
Quantum computers are often touted as the solution to all our problems. They are expected to cure disease, alleviate world hunger and even help mitigate the effects of climate change. Fuelled by this enthusiasm, a number of quantum computing firms have started joining established markets. However, despite this interest, there is still a lot of uncertainty around the near-term uses of quantum computers. A crucial question facing quantum researchers today, in both academia and industry, is a pretty fundamental one: what problems are best solved with these devices?
The publicized uses of quantum computers often hinge around an optimization problem. Optimize the supply-chain network, for example, and you have efficient manufacturing and distribution. Optimize production of fertilizers and you reduce world hunger. Optimize the placement of electric charging stations in relation to traffic and you may have an energy-efficient fleet. Even minuscule improvements in optimization can translate to significant savings in resources. For a large airline or a delivery network like FedEx, optimizing travel routes even by a mere couple of percent means an enormous reduction in fuel usage and emissions.
The hope that quantum computers will help these sectors is based on a faith that they will let us optimize these processes better than classical computers. However, the aspirations invested in quantum-enhanced optimization often seem overmatched for the current science behind it.
Optimization is hard
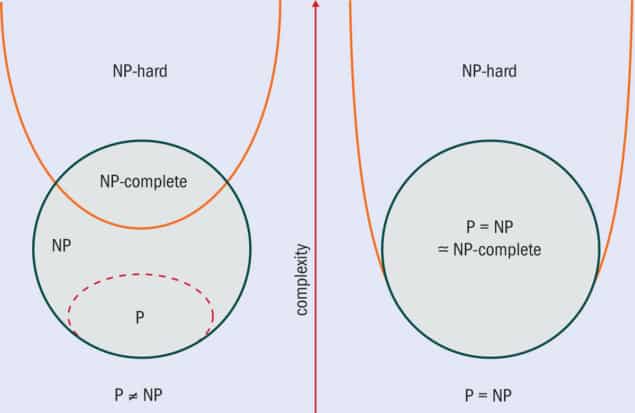
Optimization decisions, large or small, govern pretty much all aspects of our lives. The route for your Uber ride is optimized to shorten travel time. The algorithms underlying the internet optimize the flow of your data through servers. Meanwhile, banks around the world use complex financial optimizations to decrease risk. Some of these optimization decisions are easy – in the sense that an optimal solution can be found quickly by a computer algorithm. Computer scientists group these problems into a family called “P”. However, many optimization problems are difficult, with the problem of identifying the best route to deliver mail and packages – the well-known Travelling Salesman problem – being particularly hard. The reason these problems are so tough is that there is no easy way to obtain the best solution without exploring all possibilities. Many of these hard problems belong to the class “NP-hard”.
Perhaps the most exalted question in computer science is whether all problems have efficient algorithms. More popularly known as the P = NP question, it’s one of the Clay Mathematics Institute’s seven “Millennium Problems”, a proof of which would win you a million dollars. But even after more than half a century of research, there has been little progress in proving P = NP, and it seems the two classes are destined to remain separate. According to Scott Aaronson from the University of Texas, Austin, who is one of the foremost experts in complexity theory, proving P = NP would be “almost like discovering faster-than-light communication or a perpetual motion machine.”

Despite being a hard problem, we still use optimizations all the time. For many of these problems it is often enough to have a decent solution that avoids needless waste, and computer scientists have developed powerful algorithms to generate decent solutions fast. Opting for good instead of perfect makes optimization work. A pizza delivery route may not be perfect, but it is usually good enough to make sure most pizzas get delivered within a reasonable time. Researchers working in quantum optimization similarly hope that quantum algorithms might produce better solutions by exploiting quantum effects that conventional or classical computers cannot access. The most popular family of algorithms designed for such optimization goes by the name “variational quantum algorithms.”
Taking the guess out of guesswork
The variational method traces its roots to the early days of quantum mechanics, a central problem in which is finding the lowest energy or ground-state wavefunction. A wavefunction describes the configuration of a system of particles or fields and has a certain energy, determined by a mathematical object known as a Hamiltonian. Given a Hamiltonian describing, for instance, a system of electrons moving around many nuclei, we may want to find a configuration of atomic orbitals that minimizes energy, which is the configuration the molecule would occupy at low temperatures where quantum mechanical effects are more pronounced. Researchers care about the ground-state wavefunction because it describes the most stable shape or geometry of a molecule, which would be critical in, for example, designing drugs and new materials.
Solving the ground-state wavefunction can be extremely hard, even for a simple system like two electrons moving around a nucleus. Because of mathematical complications due to electrons repelling each other, the Hamiltonians of such systems do not lend themselves to analytic solutions that can be derived using pen and paper. Confronted with such an intractable problem, what physicists often do is conjure a “guess” wavefunction and calculate its energy. The guess wavefunction is then tweaked slightly to lower the energy. Repeating this process many times, varying the wavefunction at each step, we reach a solution that, hopefully, is very close to the real ground-state wavefunction. The variational technique has had such a successful run that it is a quintessential chapter in modern physics textbooks.

Variational quantum algorithms adapt the variational technique to quantum computers. It has been known for some time that quantum computers can do certain tasks, like factoring numbers, unequivocally faster than known classical algorithms. Factoring numbers is one of those problems for which we still do not have an efficient classical algorithm, and much of cybersecurity, in particular encryption, depends on this assumed computational hardness. In 1994, Peter Shor gave a blueprint of a quantum algorithm that would factorize a number quickly. However, algorithms like Shor’s need a quantum computer with many qubits as well as a very high degree of accuracy, both of which are beyond the reach of the quantum computers available today. This invites a question: is there anything useful we can do in the immediate future using noisy quantum computers with a small number of qubits?
A promising answer emerged in 2014 through a collaboration led by Alberto Peruzzo and Jarrod McClean, then at the University of Bristol and Harvard University, respectively. Inspired by the variational method popular in quantum chemistry, they proposed using a quantum computer to generate good guesses for the ground-state wavefunction of a chemical system (Nat. Commun. 5 4213). This was motivated by the belief that since nature itself is described by quantum mechanics, a guess produced by a quantum computer could offer better approximations to the real ground-state. Quantum computers operate by rotating qubits, one at a time or in groups. A quantum circuit describes a sequence of such rotations. You can construct a quantum circuit to produce a guess state and you can measure the energy of that particular guess. If you can systematically tweak the rotation parameters such as angles, you can lower the energy until it reaches a minimum. This is a variational quantum circuit.
Also in 2014, Edward Farhi and Jeffrey Goldstone from the Massachusetts Institute of Technology, together with Sam Guttman from Northeastern University, Boston, adapted the variational method to solve an optimization problem (arXiv:1411.4028). They chose a celebrated NP-hard problem, the “MaxCut” problem, which involves dividing a graph into two groups such that the number of connections between them is maximized. Farhi and his team observed that this problem can be encoded into a variational quantum circuit, which can then be used to generate systematically better guesses. The algorithm wouldn’t promise to perfectly solve the problem, but it would give a good approximate answer most of the time. Indeed, the trio showed that the solutions obtained from this quantum version of the algorithm were, on average, better than any classical algorithms known at the time. They dubbed their algorithm “quantum approximate optimization algorithm”, or simply QAOA. “It was the first time that anyone had given a quantum algorithm that gave an approximation better than a classical algorithm,” reminisces Aaronson, who was one of the first to draw attention to this work with a post on his popular blog.
Since then, researchers have applied the variational quantum technique to a plethora of optimization problems, from designing electric-vehicle charging grids to improving aircraft flights. At the core of these seemingly diverse cases are only a handful of graph-theoretic concepts, MaxCut being one of them. Researchers are still trying to consolidate the quantum advantage for such core concepts. In a more recent work, Farhi approached the Sherrington–Kirkpatrick model, another famous problem in physics and computer science that aims to minimize the energy of a system of spins. A celebrated solution developed by Giorgio Parisi, who shared the 2021 Nobel Prize for Physics, gives the minimum energy attainable by a solution to the Sherrington–Kirkpatrick model. When Farhi and his team studied this problem using computer simulations, they observed their solutions getting gradually better with repetitions of QAOA, leading them to surmise that it might actually reach the optimal limit identified by Parisi. Aaronson, however, cautions against treating tenuous numerical results on small instances of problem as credible evidence of quantum superiority, especially in light of steady advances being made with non-quantum algorithms. In fact, the original edge of QAOA over classical algorithms has vanished since its conception – the support for techniques like QAOA remains merely hypothetical.
The fault in our stars
The grand vision of using the variational quantum computer to solve hard optimization problems is not without its sceptics and detractors. Computer scientists do not expect quantum computers to solve NP-hard optimization problems efficiently. Doing so would be “almost as amazing as proving P = NP” according to Aaronson, and would likely dismantle the entire edifice of complexity theory. If you subscribe to this conviction, then it seems implausible that the variational technique would somehow give efficient solutions to problems for which there were none. Something would have to give, and only recently are we getting insights into what might derail this grand vision.
Variational algorithms “vary” a circuit to obtain approximate solutions to an optimization problem. In other words, they optimize the construction of a circuit to solve another optimization problem. It may sound convoluted, but this technique is very widely used and is extremely successful in machine learning, where the parameters in a neural network are systematically changed to lower the discrepancy between the predictions of the neural network and the training data. A helpful picture to understand this concept is that of trying to find the bottom of a valley by following the curves in the landscape. For example, a blindfolded person standing on a hilly slope can tell from the forces acting on them what direction to follow to get to the bottom of the hill – the steeper the slope, the easier it is to find the way down. Much in the same way, you can only systematically optimize the circuit or train the neural network if you can identify the direction to move for the next update. In a serious setback, in 2018, researchers at Google led by Jarrod McClean and Sergio Boixo found that the vast majority of quantum circuits are simply untrainable (Nat. Comms. 9 4812). In the language of landscapes, instead of curves one can follow, all one sees is a plateau with no indication of the direction in which a solution may lie – almost like being lost in a desert with no compass or sense of direction. This phenomenon is referred to as “barren plateaus.”
At other times, instead of reaching the bottom of a valley, it’s also possible to get stuck in a small ditch nowhere near the bottom – the variational technique, in this case, is said to be stuck in some “local minimum”. Untrainable circuits, barren plateaus and deceptive local minimas appear to be nature’s tricks preventing us from reaching solutions to hard problems. In work done in September 2021, researchers Lennart Bittel and Martin Kliesch from Heinrich Heine University Düsseldorf showed that the variational optimization process of tweaking the circuit until you arrive at some minimum is itself an NP-hard problem (Phys. Rev. Lett. 127 120502). Their results indicate that not only are variational algorithms futile against the hardest optimization problems, but the variational route remains intractable even for some problems that should be easy using other conventional techniques.
It is very possible that there are interesting problems for which variational training is efficient
This makes one wonder if variational quantum optimization might just be a really onerous and cumbersome way to solve a problem. Nevertheless, we still have some room to be wishful. It is very possible that there are interesting problems for which variational training is efficient; just because the variational technique doesn’t work for some particularly unfortunate problems doesn’t necessarily mean that it won’t be useful for an average problem we are more likely to encounter. When asked if his results preclude decent approximations to an average-case problem, Kliesch muses, “Well, that is the big question.” In fact, he suggests that there may be a way of getting around this negative result by adding more knobs to a variational circuit – by adding more qubits and running circuits for longer times – than they considered in their current work.
Noisy neighbours
Running quantum circuits to longer times, though, invites a new problem: noise. Even though the variational technique was developed for near-term noisy computers, recent research has shown that the effect of noise can be very debilitating. Indeed, Daniel França from the University of Copenhagen and Raul Garcia-Patron from the University of Edinburgh have shown that noise degrades the performance of quantum optimization algorithms so much that they are not going to be any better than very crude classical alternatives (Nat. Phys. 17 1221). According to França, the noise levels would have to go down by a magnitude of one or two compared with current levels for variational quantum methods to have a chance against classical algorithms.
Garcia-Patron notes one more obstacle: most of the quantum computers being built today have limited connectivity, that is, you can only do operations on adjacent qubits.
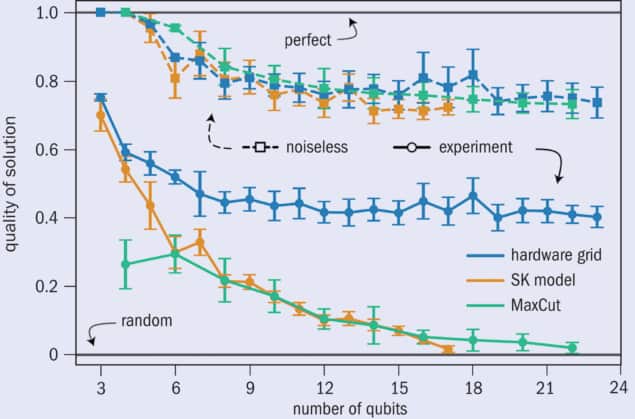
In contrast, optimization problems often demand operations between all pairs of qubits. “For many instances, the connectivity of the device will not match the connectivity of the problem, which makes noise accumulate even further,” Garcia-Patron says. In fact, when researchers at Google recently implemented Farhi’s new quantum solution to the Sherrington–Kirkpatrick model on their Google Sycamore superconducting qubit quantum processor, they noticed that the performance degrades strongly with noise (Nat. Phys. 17 332) (figure 1). França and Garcia-Patron studied the work from Google very closely and found that “their decay is consistent with our predictions.”
Despite the pessimism of complexity theorists, as well as the difficulties with noisy hardware, researchers in quantum optimization remain hopeful that each of these obstacles can be addressed one by one. Circuits untrainable because of barren plateaus? There has been steady progress on algorithms that get around these. Too much noise? Quantum hardware has been gradually improving for the last couple of decades – give us a few more years and we might get to noise-resistant quantum computers. In fact, fault-tolerant qubits have been demonstrated by several labs around the world. It just remains to scale fault-tolerance to a large number of qubits.
“Perhaps variational algorithms will be the first useful algorithms of the fault-tolerance era,” surmises Garcia-Patron. The biggest challenge against variational quantum optimization is really the one originating in complexity theory. There is a mathematical chasm separating quantum computers from the optimization problems we would like to solve with them. Unlike the case with noise, there has been no progress in bridging this chasm for more than half a century, and it is possible that it may never happen.
Quantum computers have even faltered in the easier job of finding approximate solutions. When Farhi, Goldstone and Gutmann first provided a quantum algorithm that attained a higher approximation ratio (a measure of how close solutions are to the optimal solution) than classical algorithms for solving MaxCut, computer scientists responded by discovering a classical algorithm with an even higher approximation ratio. The quantum advantage for MaxCut was only ephemeral. Since then, there has been an ongoing dance between quantum researchers claiming a quantum advantage on hard problems and computer scientists trying to develop even better classical algorithms to surpass the claims made by quantum researchers.

Even with the Sherrington–Kirkpatrick model that Farhi and his team at Google studied, Aaronson points out that there is a classical algorithm developed in 2018 that is already conjectured to reach the optimal value identified by Parisi. The debate continues and, as of now, we do not have strong evidence to believe that quantum optimization techniques have any definite advantage over good classical alternatives. “We still do not have a killer example where we are confident that QAOA reaches a certain approximation ratio and we are confident that a classical algorithm does not. It remains an excellent open question,” explains Aaronson.
To be sure, similar criticism can be levelled against deep learning and artificial intelligence, where we do not always have provable performance guarantees. Yet, deep learning has yielded astoundingly successful results in the last decade. Machine learning did not get to this stage overnight; it had to wait until computer processors were powerful enough to run deep neural networks. “Optimizing a unit in a neural network is also NP-hard,” says Kliesch, noting that complexity theoretic hardness doesn’t necessarily prevent usefulness and that quantum optimization could follow a similar arc. Indeed, if quantum algorithms work well in practice, perhaps the search for a provable quantum advantage would be misguided and there would be a strong justification for using quantum optimization.
What’s more, not only do we not have large enough quantum computers to test algorithms on, it is also notoriously hard to study a quantum algorithm using simulations. Even the most powerful supercomputers struggle to simulate a quantum algorithm on more than 50 qubits. Whatever research we have on quantum optimization comes from studies of very small problems. In some of those studies, quantum algorithms look promising, but we will have to test these algorithms on large instances of similar problems to be sure.
Reading the fine print
The world of quantum optimization is rife with speculation, conjectures and convictions. We have a novel technology whose promises are difficult to ascertain or debunk. Since the formulation of QAOA in 2014, there has been an enormous amount of interest in solving industrial optimization problems, leading to a slew of research collaborations and publications. According to Aaronson, this volume of interest might be deceptive. “There is a pathology where there have been hundreds of papers over the past six or seven years about QAOA, creating an impression to an outsider that there is a quantum speedup when there is none. That is, at best, harmless,” he says, adding that one has to be aware of the caveats and fine print while assessing new research.
There is, nevertheless, one point on which everyone seems to agree: it is very likely that some problems exist where quantum optimization is provably superior to classical methods, but these problems will likely occur in the realm of physics and not in finance or industrial operations. “Nature is quantum. If nature can solve a problem, so should quantum computers,” says França, who is confident about problems involving molecules or quantum materials like superconductors. “The strongest case for variational algorithms,” Aaronson says, “seems to be on problems that are themselves quantum.”
Collected at: https://physicsworld.com/a/conquering-the-challenge-of-quantum-optimization/

buy generic cialis https://pudbiascan.strikingly.com/
Kudos, A good amount of knowledge.